Quelle est la valeur relative du nombre ?

Dans cette pièce, nous montrerons comment Arduino peut percevoir le temps. Nous examinerons plus en détail les fonctionnalités d’attente (délai) et plus encore. Ensuite, nous montrerons les possibilités des opérations mathématiques et, en conclusion, imaginons des fonctions pour générer des nombres aléatoires.

Heure

En équipement de base, les cartes Arduino ont quatre fonctions pour travailler avec le temps. Il s’agit des fonctions DelayMicroseconds (), DelayMicroseconds (), millis () et micros (). Les deux premiers et les deuxièmes fonctionnent sur le même principe, en travaillant uniquement avec d’autres unités. C’est des millisecondes et des microsecondes. Il est important de rappeler la relation de conversion entre les unités de temps lorsque : 1 seconde = 1 000 millisecondes = 1 000 000 microsecondes.

Lire également : Les clés d'une stratégie marketing efficace grâce à l'intelligence artificielle

retard ()

Nous avons déjà rencontré cette fonctionnalité. Il a un seul paramètre, à savoir le temps d’attente en millisecondes. La plage de paramètres est comprise entre 0 et 4 294 967 295. Le grand inconvénient de la fonction de délai ainsi que la fonction suivante DelayMicroseconds () est le fait qu’il y aura un arrêt presque toutes les activités (suspension des valeurs de lecture des capteurs, impossibilité de contrôler les valeurs logiques sur les broches, etc.). Cependant, il n’y aura pas d’arrêt des fonctionnalités qui ne sont pas directement dépendantes du processeur. C’est surtout la réception des informations de la ligne Rx, lorsque les appartements acceptés sont remplis avec le tampon et que le traitement ne se produit qu’après la fonction de retard est terminée, ainsi que la fonction AnalogWrite (). En fait, la génération de signaux PWM se déroule en dehors du bloc principal du processeur.

int cejseconds = 1 ; longs cekejmiliseconds = cejsecond*1000 ; void setup () { PinMode (13, OUTT) ; } boucle void () { retard (cejmiliseconds) ; DigitalWrite (13, ÉLEVÉ) ; retard (cejmiliseconds) ; DigitalWrite (13, FAIBLE) ; } DelayMicrosecondes ()

La fonction est similaire à delay (), seulement avec la différence que le paramètre est le temps en microsecondes. La plage de paramètres est comprise entre 0 et 65 535.

Lire également : Améliorez votre stratégie marketing grâce à l'intelligence artificielle

millis ()

En utilisant la fonction millis (), on peut déterminer la valeur stockée dans la Minuteries CPU. Voici conservé des informations sur la durée d’exécution du programme depuis son lancement. Ainsi, cette fonction n’a besoin d’aucun paramètre et renvoie le nombre de millisecondes depuis le début du programme. Cependant, ce nombre n’est pas infini. La valeur maximale de retour est de 4 294 967 295. Après la traversée, il y aura un soi-disant débordement de minuterie, qui commence alors à compter à nouveau à partir de zéro. La fonction millis () est utilisée, par exemple, où il est nécessaire d’attendre, mais il n’est pas souhaitable que le fonctionnement du programme soit interrompu.

//programme qui envoie chaque seconde un message sur le nombre de ms après la ligne série cas longs non signés = 0 ; void setup () { serial.begin (9600) ; } boucle void () { if (millis () >

= cas 1000) { cas = millis () ; serial.println (cas) ; } } Note : Le débordement du minuteur se produit environ une fois tous les 50 jours. (4 294 967 ms = 4 294 967 s = 71 582 min = 1193 h = 49,7 jours)

micros ()

La fonction micros () est la même que millis (), renvoie uniquement en microsecondes. La plage de valeurs est la même, mais puisque 1 milliseconde = 1000 microsecondes, le temps de débordement sera des milliers de fois plus petit, c’est-à-dire environ 71,5 minutes. Il faut ajouter que la résolution de la fonction est de 4 microsecondes pour les processeurs 16 MHz et 8 MHz 8 microsecondes. Ainsi, la sortie de la fonction sera un multiple de quatre, ou huit.

Remarque : Vous pouvez vous demander pourquoi les valeurs maximales des paramètres, ou nombres renvoyés, sont ce qu’ils sont. C’est le cas parce que les fonctions de travail du temps utilisent deux types de données que je n’ai pas répertoriés dans l’article Structures de base de câblage. Ils sont non signés int et non signés long. Le type de données int non signé a la même plage de valeurs que int, seule cette plage est déplacée vers des nombres positifs. Le type int peut conserver des nombres de 32 768 à 32 767. Le type int non signé ne fonctionne pas avec des nombres négatifs. La plage est donc de 0 à 65 535. La même situation est avec non signé long, seulement avec une plus grande plage.

Mathématiques

fonction Maintenant, montrons quelles opérations mathématiques Arduino prend en charge. Mais avant de commencer, rappelons-nous les opérateurs de base.

Opérateurs mathématiques

La plupart de ces opérateurs sont bien connus de nos classes de mathématiques. La seule exception est l’opérateur% (modulo), qui renvoie le reste après la division entière.

1 2 = 3 //addition 2 – 1 = 1 //soustraction 2 * 3 = 6 //multiplication 9/3 = 3 //division //modulo 9 % 6 = 3 //à première vue, cette opération est tout à fait spéciale //mots peuvent être simplement indiqués comme : 9 divisé par 6 est 1 reste 3 //opération modulo nous retournera ce repos L’ utilisation pratique se trouve par le fonctionnement modulo, entre autres choses, dans la détermination de la divisibilité. Si le résidu après division et le numéro b est nul, alors il est divisible par b.

int a = 20 ; int b = 5 ; if (a% b == 0) { //a est divisible par b } autre { //a pas divisible par b } min ()

La fonction min est utilisée pour sélectionner un nombre plus petit. Les paramètres d’entrée sont deux nombres et la valeur de sortie du plus petit d’entre eux. Il est utilisé, par exemple, lors de la recherche du plus petit nombre dans un tableau, ou pour restreindre les valeurs d’un capteur (afin de ne pas dépasser une certaine limite).

//trouver le plus petit nombre dans le tableau void setup () { int delka = 10 ; champ int = {2, 4, -8, 3, 2, 100, 200, 50, 99, 358} ; int nejm = tableau ; //le plus petit nombre serial.begin (9600) ; pour (int i = 1 ; i <

delka ; i ) { nejm = min (nejm, champ) ; } serial.println (nejm) ; } boucle void () { } max ()

La syntaxe de cette fonction est identique à min (). Ses paramètres sont également deux nombres, et la valeur renvoyée est la plus grande d’entre eux. Il peut être utilisé, par exemple, à la recherche du plus grand nombre dans le

//rechercher le plus grand nombre dans le tableau void setup () { int delka = 10 ; champ int = {2, 4, -8, 3, 2, 100, 200, 50, 99, 358} ; int nejm = tableau ; //plus grand nombre serial.begin (9600) ; pour (int i = 1 ; i <

delka ; i ) { nejm = max (nejm, champ) ; } serial.println (nejm) ; } boucle void () { } abs ()

Cette fonction renvoie la valeur absolue du nombre. Ainsi, l’entrée est le nombre et la sortie de sa valeur absolue.

Note : La valeur absolue du nombre x est un nombre réel non négatif. Si x > = 0, abs (x) = x. Si x est < 0, alors abs (x) = -x. En termes profanes, la valeur absolue est la distance d'un nombre par rapport à zéro sur l'axe des nombres.

x = abs (150) //x = 150 x = abs (-150) //x = 150 contrainte ()

Nous pouvons imaginer cette fonction comme une combinaison de min () et max () avec des paramètres appropriés. Il sert à limiter la plage de la variable à la fois d’en haut et en bas. Il a trois paramètres : la valeur ajustée, la limite inférieure et la limite supérieure. Si le numéro d’entrée tombe en dessous de la limite inférieure, la sortie est la valeur de la borne inférieure. Si elle dépasse la limite supérieure, la valeur résultante est limite supérieure. Si la valeur est dans les limites, la sortie de la fonction sera la même que sur le paramètre d’entrée.

x = contrainte (valeur ajustée, limite inférieure, limite supérieure) ; x = contrainte (1,10,100) ; //x = 10 x = contrainte (150, 10, 100) ; //x = 100 x = contrainte (50, 10, 100) ; //x = 50 cartes ()

Comme la fonction constrain (), la fonction map () sert à modifier la plage d’une variable. Contrairement à la fonction précédente, cependant, il n’y a pas de coupe de valeurs mais même « étirement », ou « presser » toute l’échelle. Par exemple, il peut être utilisé pour modifier la valeur obtenue à partir de la lecture de l’entrée analogique (0 — 1023) et les utiliser dans AnalogWrite, qui fonctionne avec des valeurs comprises entre 0 et 255. La syntaxe est la suivante : x = map (valeur, MinimOriginal Scale, MaximumOriginal Scale, MinimNew Scale, MaximumNew Scale) ;

//réglage de la luminosité des LED à l’aide d’un potentiomètre int analogique, pwm ; void setup () { serial.begin (9600) ; } boucle void () { analogique = analogEad (A0) ; pwm = carte (analogique, 0, 1023, 0, 255) ; Sérial.print (« Analogique : « ) ; sérial.print (analogique) ; Serial.print ( » PWM : « ) ; serial.println (pwm) ; AnalogWrite (11, pwm) ; } pow ()

Fonction pour alimenter un nombre à un autre nombre. Les paramètres d’entrée sont le nombre et la racine.

pow (10,3) = 1000 ; pow (10,4) = 10000 ; pow (2,5) = 32 ; //utiliser la démonstration int a = 10 ; int b = 3 ; flotteur c ; void setup () { serial.begin (9600) ; } boucle void () { c = pow (a, b) ; serial.println (c) ; retard (1000) ; } sqrt ()

La fonction sqrt () renvoie la racine carrée du numéro d’entrée.

sqrt (25) = 5 ; sqrt (256) = 16 ; sqrt (10000) = 100 ; Fonctions goniométriques

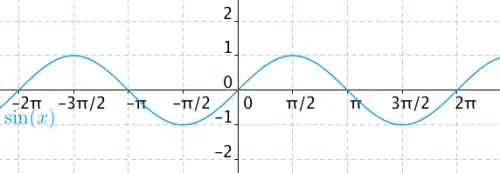
Avant d’imaginer des fonctions individuelles, parlons des unités d’angles. Nous sommes principalement habitués à mesurer l’angle en degrés. L’angle complet ici est de 360°. Mathématiquement plus précis, cependant, est l’utilisation de radians. Ces unités sont basées sur cercles d’unité. Plein angle (360°) est égal à 2*PI de radians, 180° = PI de radians, etc. La relation de transfert s’applique entre eux : radians = (degrés * PI) /180. Les fonctions goniométriques trouvent une application dans le calcul des côtés et des angles dans les triangles et autres formations planaires et spatiales. Toutes les fonctions goniométriques sont périodiques — après un certain intervalle, leurs valeurs sont répétées.

péché ()

La valeur fonctionnelle de la fonction sinusoïdale est donnée comme le rapport du côté opposé à l’hypoténuse dans un triangle droit. L’amplitude de la fonction est 1 et la période 360°, ou 2PI de radians. Le graphique de la fonction est le soi-disant sinusoida. Le paramètre de la fonction est l’angle en radians, et la valeur de sortie est la valeur du sinus pour un angle donné. L’exemple suivant répertorie la partie du sinusoïde tourné à 90° en utilisant des traits d’union sur la ligne série.

fonction sinusoïdale

flotteur pi = 3.14159265359 ; int amplitude = 10 ; //être un sinusoïde visible, nous augmentons son amplitude 10x période de flotteur = 2*pi ; valeur flottante ; void setup () { serial.begin (9600) ; //ce cycle trouve la valeur de la fonction sinusoïdale après les décimales de PI pour (flotteur i = 0 ; i